Giovanni Girolamo Saccheri
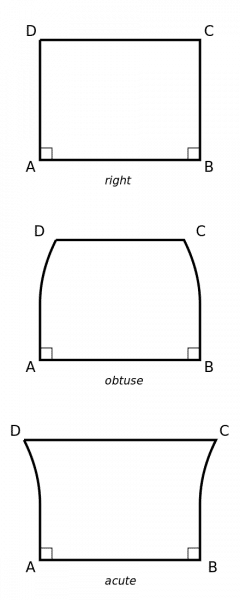
Giovanni Girolamo Saccheri, S.J. (September 5, 1667 to Octember 25, 1733) Saccheri was a Jesuit priest and mathematician. He is famous for discovering many theorems of non-Euclidean geometry. As did many people before and after him, Saccheri tried to prove Euclid’s famous “fifth postulate,” which says that “through any point not on a given line there is one and only one line that is parallel to the given line.” Saccheri attempted to prove this “by contradiction,” that is by showing that one is led to a contradiction if one assumes that Euclid’s fifth postulate is false. In trying to find such a contradiction, Saccheri ended up deriving many remarkable theorems that follow from denying the postulate, and these are now understood to be theorems of “non-Euclidean geometry” (specifically, hyperbolic geometry). Though Saccheri could not find the logical contradiction he was looking for (there isn’t any), he apparently could not bring himself to believe that the non-Euclidean theorems he was exploring were really self-consistent. (Or at least, he was not willing to make that claim.) As a result, he narrowly missed being the discoverer of hyperbolic non-Euclidean geometry. That honor belongs to Gauss, Taurinus, Lobachevsky, and Bolyai about 100 years later. Saccheri’s work went unnoticed until the mid-nineteenth century, when his writings on the subject were rediscovered by the famous Italian mathematician Eugenio Beltrami. The “Saccheri Quadrilateral,” an important diagram in non-Euclidean geometry, is named after him. (See figures on the left.)
Explore Other Scientists
It is our hope that this curated set of biographies will be useful to teachers, students, and the general public.